संख्या पद्धति(number system)
संख्या पद्धति(number system)
0, 1, 2, 3 ,4……..etc को हम संख्याएं (number) कहते है।संख्याओं को लिखने और संख्याओं के नामकरण को व्यवस्थित करने की प्रक्रिया को संख्या पद्धति कहते है।
संख्या पद्धति में हम 0 से लेकर अन्नत तक कि संख्याओं के बारे में पड़ते है और संख्याओं को किस तरह कितने वर्गों में बंटा गया है वह जानकारी समझकर संख्याओं का उपयोग करना सीखते है।
वेबसाइट के बारे में:-
आपका इस वेबसाइट पर स्वागत 🙏🙏🙏🙏🙏🙏है इस पोस्ट में आप संख्या पद्धति संबंधित जानकारी पाएंगे,आपकी जानकारी के लिए बताना चाहूंगा कि purijaankarifree.blogspot.com नए आर्टिकल पोस्ट किए जाते हैं इसलिए आप रोज इस वेबसाइट पर आते रहे हैं जिससे आप कोई भी महत्वपूर्ण टॉपिक ना छूटे
हम इस पोस्ट में संख्या पद्धति संबधित लगभग सभी टॉपिक्स को कवर किया गया है जो आपको प्रतियोगिता में अच्छे मार्क्स लाने में मदद करेंगे
अगर आपको कोई भी सुझाव देना चाहते हैं तो आप कमेंट बॉक्स में अपने मैसेज डाल सकते हैं हम आपके मैसेज का रिप्लाई 24 घंटे के में दे देंगे
जारी रखें:-
हम संख्याओं के प्रकारों को विस्तार में समझते हैं।
💎 प्राकृतिक संख्याएं :
गिनती में उपयोग की जाने वाली सभी संख्याएं प्राकृतिक संख्या कहलाती हैं ।
Ex: 1, 2, 3, 4, 5, ………
💎 सम संख्याएं
ऐसी प्राकृतिक संख्या जो 2 से पूर्णतः विभाजित होती हैं, उन्हें सम संख्या कहा जाता हैं
Ex: 2, 4, 6, 8, 10, ………
💎 विषम संख्याएँ
ऐसी प्राकृतिक संख्या जो 2 से पूर्णतः से विभाजित न हो उन्हें विषम संख्या कहते हैं।
Ex: 1, 3, 5, 7, 9, 11, ………
💎 पूर्णांक संख्याएँ
धनात्मक त्रणात्मक और जीरों से मिलकर बनी हुई संख्याएँ पूर्णांक संख्या होती हैं।
ये तीन प्रकार की होती हैं।
धनात्मक संख्याएँ : एक से लेकर अनंत तक की सभी धनात्मक संख्याएँ धनात्मक पूर्णांक हैं।
त्रणात्मक संख्याएँ : 1 से लेकर अनंत तक कि सभी त्रणात्मक संख्याएँ त्रणात्मक पूर्णांक हैं।
उदासीन पूर्णांक : ऐसा पूर्णांक जिस पर धनात्मक और त्रणात्मक चिन्ह का कोई प्रवाह ना पड़े। और यह जीरो होताा है
Ex: -3, -2, -1, 0, 1, 2, 3, ………
💎 पूर्ण संख्याए
प्राकृतिक संख्याएँ में 0 से सामिल कर लेने से पूर्ण संख्या बनती हैं।
Ex: 0, 1, 2, 3, ………
💎 भाज्य संख्या
ऐसी प्राकृत संख्या जो स्वंय और 1 से विभाजित होने के अतिरिक्त कम से कम किसी एक अन्य संख्या से विभाजित हो उन्हें भाज्य संख्या कहते हैं।
Ex: 4, 6, 8, 9, 10, 12, ………
💎 अभाज्य संख्याए
ऐसी प्राकृतिक संख्याएँ जो सिर्फ स्वंय से और 1 से विभाजित हो और किसी भी अन्य संख्या से विभाजित न हो उन्हें अभाज्य संख्याएँ कहेंगे।
Ex. 2, 3, 5, 11, 13, 17, ………
💎 सह अभाज्य संख्या
कम से कम 2 अभाज्य संख्याओ का ऐसा समूह जिसका (HCF) 1 हो।
Ex. (5, 7) , (2, 3)
💎 परिमेय संख्याएँ
ऐसी सभी संख्याएँ जिन्हें p/q के रूप में लिखा जा सकता हैं। उन्हें परिमेय संख्याएँ कहते है
(q हर का मान जीरो नहीं होना चाहिए)
Ex: 5, 2/3, 11/4, √25
💎 अपरिमेय संख्याएँ
ऐसी संख्याएँ जिन्हें p/q के रूप में नही लिखा जा सकता और मुख्यतः उन्हें (”√”) के अंदर लिखा जाता हैं। और कभी भी उनका पूर्ण वर्गमूल नहीं निकलता।
Ex: √3, √105, √11, √17,
नोट:-(π एक अपरिमेय संख्या हैं।)
💎 वास्तविक संख्या
परिमेय और अपरिमेय संख्याओ को सम्मलित रूप से लिखने पर वास्तविक संख्याएँ प्राप्त होती हैं।
Ex: √3, 2/5, √15, 4/11,
💎 अवास्तविक संख्या (कल्पनिल संख्या)

यह एक काल्पनिक संख्या है
संख्या पद्धति के महत्वपूर्ण प्रश्न
प्राकृतिक संख्याओं का योग = ( पहली संख्या + अंतिम संख्या / 2) × n
जहाँ N = ( अंतिम संख्या – पहली संख्या / वर्ग अंतराल)
Q. 1+2+3+4 ……… 58+59+60 = ?
हल:- according to question
1+2+3+4 ……… 58+59+60
अंतिम संख्या(last number) = 60
प्रथम संख्या(frist number) = 1
N = (अंतिम संख्या – पहली संख्या)/वर्ग अंतराल + 1
=N = ( 60 – 1 ) / 1 + 1
=N = 59 + 1
=N = 60
=योग = ( पहली संख्या + अंतिम संख्या / 2 ) × n
=योग = (1 + 60 ) / 2 × 60
=योग = 61 × 60 / 2
=योग = 61 × 30
=योग = 1830
प्रथम n प्राकृत संख्याओं के वर्गों का योग = n(n+1)(2n+1)/6
Q. 1 से 32 तक की सभी प्राकृतिक संख्याओं के वर्गों का योग बताइये
हल: according to question
n = 32
=योग = n (n + 1) (2n +1 ) / 6
=योग = 32 (32 + 1)(2 × 32 + 1) / 6
=योग = 32 × 33 (64 + 1) / 6
=योग = (32 × 33 × 65) / 6
=योग = 16 × 11 × 65
=योग = 11,440
Ans. 11,440
प्रथम n प्राकृत संख्याओं के घनों का योग = [n(n+1)/2]^2
Q.1 से 90 तक की सभी प्राकृत संख्याओं के घनों का योग क्या हैं?
हल:-according to question
=[n (n + 1) / 2]² where , n = 90
=[90 (90 + 1) / 2]²
=(90 × 91 / 2)²
=( 8190 / 2)²
=(4095)²
=1669025
Ans. 1669025
भाज्य = ( भाजक × भागफल ) + शेषफल
भाज्य – शेषफल = भाजक × भागफल
भाज्य – शेषफल / भागफल = भाजक
Q.किसी भाग के प्रश्न में भागफल 403 हैं और यदि भाजक 100 हैं, एवं शेषफल 58 हैं तो भाज्य कितना हैं?
हल:- भाज्य = (भाजक × भागफल) + शेषफल
=(100 × 403) + 58
=40300 + 58
=40358
Ans. 40358
Q. दो संख्याओं का योगफल 14 एवं अंतर 10 है दोनों संख्याओं का गुणनफल क्या होगा ?
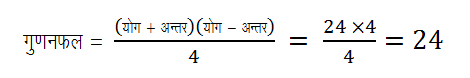
Q. वह न्यूनतम संख्या ज्ञात कीजिये जिसमें 9, 11, एवं 13 से भाग देने पर क्रमश: 1, 3, 5 शेष बचते हों?

=1258-8 = 1250
Q. वह सबसे बडी संख्या ज्ञात कीजिये जिससे 55, 127 एवं 175 से भाग देने पर प्रत्येक दशा में समान शेष बचे

Q. 5 अंकों की वह बडी से बडी संख्या कौन सी है जो 137 से पूर्णत: विभक्त हो जाये?

जानवरों की संख्या पर आधारित प्रश्न(animals numbers based question)
चार पैर वालों की संख्या = (पैर / 2) – सिर
दो पैर वालों की संख्या = सिर – चार पैर वालों की संख्या
Q. गड़िया अपनी भेड़े चढ़ा रहा था यदि जमीन पर पैरों की कुल संख्या 230 हैं और सिरों की कुल संख्या 60 हैं तो बताये उसके पास भेड़ों की कुल कितने
हल:-
चार पैर वालों की संख्या = (पैर / 2) – सिर
=(230 / 2) – 60
=115 – 60
=55
Ans. 55
संख्याओं पर आधारित प्रश्न( based on number)
Q.किसी संख्या का 2/3 का 3/4 का 4/5 यदि 420 हैं तो वह संख्या क्या हैं?
हल:- प्रश्नानुसार,
=1 × 2/3 × 3/4 × 4/5 = 420
=1 × 2/5 = 420
=1 = 420 × 5 / 2
=1= 210 × 5
=1050
इकाई अंक पर आधारित प्रश्न( unit bases question)
💧इकाई के स्थान पर यदि 0 होगा तो इकाई का अंक 0 होगा।
Ex-
💧इकाई के स्थान पर यदि 1 होगा तो इकाई का अंक 1 होगा।
💧इकाई के स्थान पर यदि 5 होगा तो इकाई का अंक 5 होगा।
💧इकाई के स्थान पर यदि 6 होगा तो इकाई का अंक 6 होगा।
वर्गमूल (Square Root)
दाई ओर से दो अंको का जोड़ा बनाये और शेष बचे (reamaning)सभी अंको का एक जोड़ा बनाये।
संख्या में दिया इकाई(unit) किसी संख्या का वर्गमूल करने पर प्राप्त होगी यह पता लगाएं और उसे उत्तर में सबसे अंत में लिखे।
शेष अंको के जोड़े से बनी हुई संख्या के सबसे नजदीक आने वाली ऐसी संख्या जिस संख्या का वर्ग हो उसे उत्तर में बाई ओर लिखे।
यदि ऐसी स्थिति में दो संख्या प्राप्त हो तो उनके बीच इकाई अंक 5 वाली संख्या का वर्ग करके दी गई संख्या से तुलना करें, तुलना करने पर दी गई संख्या छोटी संख्या हैं,
उत्तर छोटा होगा और दी गई संख्य तुलना(compare) करने पर बड़ी संख्या प्राप्त हो तो उत्तर बड़ा होगा।
Q.√11236 का वर्गमूल क्या होगा
Ans. 106
Q.√8281 का वर्गमूल क्या होगा?
Ans. 91
Q. √9216 का वर्गमूल क्या होगा?
Ans. 96
Q.√1681 का वर्गमूल क्या होगा?
Ans. 41
Q.√21025 का वर्गमूल क्या होगा?
Ans. 145
घनमूल (Cube Root)
दी गई संख्या में दाई (right) और से तीन अंको का जोड़ा(add) बनाये और शेष अंको का जोड़ा बनाएं।
दी गई संख्या में इकाई अंक जिस संख्या का घन करने से प्राप्त होगा वह संख्या उत्तर में सबसे अंत(last) में लिखे।
शेष अंकों (remainig number) के जोड़े से बनी हुई संख्या जिस संख्या के घन करने से उसके सबसे नजदीक(near) पहुँचे वह संख्या उत्तर में बाई (left) ओर लिखे।
Q.√110592 का घन मूल (cube root) कितना होगा?
Ans. 48
Q. √238328 का घन मूल(cube root) कितना होगा?
Ans. 62
Q. 785 को पूर्ण वर्ग बनाने के लिए उसमें न्यूनतम कौन सी संख्या जोड़ी (addtional)जानी चाहिए?
Ans. 56
Q. यदि 12 के घन से 22 का वर्ग घटाया जाए तो कितना आएगा?
Ans. 1244
Q.1020 को पूर्ण वर्ग बनाने के लिए क्या जोड़ा (addtion) जाना चाहिए?
Ans. 4
Q.कोई संख्या 779 से विभाजित करने पर 47 शेष बचती हैं, तो उसी संख्या को यदि 19 से विभाजित करने पर वह कितना शेष बचेगा?
Ans. 9
Q. एक संख्या का 65%, उस संख्या के भाग से 21 कम है । वह संख्या कितनी है ?
(a) 140 (b) 70 (c) 65 (d) 21
Q. माना 22 + 42 + 62 + ... + 402 = 11480, तो 12 + 22 + 32 + ....... + 202 का मान(value) क्या होगा ?
a. 2869 b.2867 c.2868 d.2870
Q.1 से 100 तक की संख्याों के सभी अंकों का योग है
a. 505 b. 903 c. 901 d.900
a. 51 b.52 c.53 d.54
Q. 584 x 128 x 617 x 413 में इकाई का अंक(unit number) क्या होगा ?
a.2 b.3 c.4 d.5
Q. (3127)173 का इकाई का अंक(unit number) क्या है ?
a.1 b.3 c.7 d.9
Q. 3k + 1 रूप की प्रत्येक अभाज्य संख्या को 6m + 1 (k, m पूर्ण संख्याएँ हैं) के रूप में निरूपित (show of indicate) किया जा सकता है, जबकि
a.k विषम है
b.k सम है
C.k विषम और सम दोनों हो सकता है
d.इस प्रकार का कोई रूप सम्भव नहीं है
Q. 34798 के विस्तार में अंतिम अंक(last number means unit number) क्या है ?
a.1 b.3 c.7 d.9
Q. 2467)153 x (341)72 के गुणनफल में इकाई का अंक (unit number) कितना होगा ?
a.1 b.3 c.7 d.9
Q. (264)102 + (264)103 में इकाई का अंक(unit number) क्या होगा ?
a.0 b.4 c.6 d.8
Q. संख्या(number) 2784936, निचे दी गई संख्याओं में से कौन-सी एक से विभाज्य(divide) है ?
a.86 b.87 C.88 d.89
Q. को 107 बार गुना किया जाता है। गुणनफल में इकाई के स्थान पर आने वाला अंक है
a.1 b.5 c.7 d.9
इनमें से कोई नहीं
Q. 50 से 1000 के मध्य पड़ने वाली पूर्ण वर्ग (square root) संख्याओं की संख्या होगी –
(a) 21 (b) 22 (c) 23 (d) 24
(a) 500 (b) 120 (c) 150 (d) 160
Q.चार अंकों वाली सबसे छोटी पूर्ण वर्ग संख्या है
(a) 1009 (b) 1016 (c) 1024 (d) 1025
Q. 2250, 3150, 5100, तथा 4200 संख्याओं में सबसे छोटी संख्या कौन-सी है ?
(a) 2250 (b) 5100 (c) 3150 (d) 4200
Q. 50 को दो भागों में विभाजित करें, जिससे उनके व्युत्क्रमो का योगफल ....... हो ।
Q. 250, 430, 340, और 520 में सबसे बड़ी संख्या है –
(a) 250 (b) 340 (c) 430 (d) 520
Q. लघुतम अभाज्य संख्या क्या है ?
(a) 3 (c) 2 (c) 123 (d) 139
Q. वह संख्या ज्ञात कीजिए, जिसका 1/7भाग उसके 1/11भाग से 100 अधिक है –
(a) 1925 (b) 1825 (c) 1540 (d) 1340
Q. ऊँटों के एक झुंड का जंगल में देखा गया । झुंड के वर्गमूल का दोगुना पहाड़ों पर चला गया । शेष 15 ऊंट नदी के किनारे देखे गये । बताइए कुल ऊँटों की संख्या कितनी थी ? कुल ऊँटों की संख्या कितनी थी ?
(a) 60 (b) 20 (c) 36 (d) 72
अगर आपके पास संख्या पद्धति से जुड़े हुए नोट्स है वो भी हमें आप भेज सकते है जिससे और लोगो की मदद हो सके ।
कोई सुझाव देना चाहते हैं तो आपका स्वागत हैं।
⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️
पीडीएफ डाउनलोड करने के लिए यहां क्लिक करें
आशा aa हूं कि आपको यह पोस्ट संख्या पद्धति अच्छी लगी होगी !
आपको यह पोस्ट अच्छी लगी है तो आप इस पोस्ट को अपने फेसबुक व्हाट्सएप इंस्टाग्राम पर शेयर करें और अपने दोस्तों को भी इस वेबसाइट के बारे में बताएं!
धन्यवाद!!!🙏🙏🙏🙏🙏🙏🙏







0 Comments
Please do not entre any spam link in the comment box,
If you need any types of solution and want to ask any types of questions to us then comment below .....